TIỀM NĂNG PHÁT TRIỂN TƯ DUY HÌNH HỌC CHO TRẺ EM THÔNG QUA TRÒ CHƠI TRÍ UẨN (Phần 1)

TIỀM NĂNG PHÁT TRIỂN TƯ DUY HÌNH HỌC CHO TRẺ EM THÔNG QUA TRÒ CHƠI TRÍ UẨN

Tác giả: Chu Cẩm Thơ, Viện Khoa học Giáo dục Việt Nam

Vũ Anh Tuấn, Công ty Cổ phần phát triển Giáo dục POMATH

Nguyễn Tiến Đạt, Công ty Cổ phần phát triển Giáo dục POMATH

1. Mở đầu

Theo Nguyễn Mạnh Tuấn [16], bản chất hình học là khoa học nghiên cứu về các tính chất của đối tượng không gian (những đặc điểm về kích thước: chiều dài, chiều rộng, chiều cao, …) và quan hệ không gian (vị trí của đối tượng được biểu thị bằng những khái niệm trong phương hướng: trước – sau, trên – dưới, trái – phải, về khoảng cách: gần – xa, …). Khi học hình học, ngoài việc sử dụng các thao tác tư duy chung như phân tích, tổng hợp, cụ thể hóa, trừu tượng hóa, khái quát hóa, tương tự hóa, thì trẻ còn tiến hành các hoạt động trí tuệ khác như xoay hình, di chuyển hình, lật hình, phóng to, thu nhỏ hình trong óc, … nhằm giải quyết vấn đề, các hoạt động này gọi chung là tư duy hình học. Câu hỏi đặt ra là: “Liệu có công cụ nào phù hợp để đo lường và phát triển tư duy hình học cho trẻ hay không?”. Trong quá trình nghiên cứu bộ trò chơi Trí Uẩn – một loại Tangram gồm 7 mảnh ghép, chúng tôi nhận thấy các quan hệ vuông góc, quan hệ song song, quan hệ bằng nhau và quan hệ đối xứng xuất hiện trên bộ trò chơi này. Chúng tôi đã tiến hành nghiên cứu, thử nghiệm và nhận thấy tiềm năng phát triển tư duy hình học ở trẻ em có thể khai thác được từ bộ trò chơi Trí Uẩn thông qua những hoạt động phù hợp.

2. Nội dung nghiên cứu

2.1 Tư duy hình học

Trên thế giới có nhiều nghiên cứu về các loại hình tư duy xuất hiện trong hoạt động hình học với những tên gọi khác nhau như: tư duy hình học (geometric thinking), tư duy không gian (spatial thinking), trí thông minh không gian (spatial intelligence), tư duy thị giác (visual thinking), tiềm năng không gian (spatial ability).

Theo L.L.Thurstone [15], tư duy không gian (spatial thinking) là một bộ phận của tư duy thị giác (visual thinking). Trong đó, tư duy không gian được thể hiện bởi ba thành tố S1, S2 và S3.

S1: Năng lực nhận biết đặc điểm một vật thể khi nó được nhìn dưới các góc độ khác nhau.

S2: Năng lực hình dung sự vận động hoặc sự dời chỗ các bộ phận bên trong của một hình thù.

S3: Năng lực xem xét về các mối quan hệ không gian, trong đó bộ phận căn bản của bài toán là hướng xoay của cơ thể người quan sát.

Các đánh giá về tư duy không gian của con người trong nghiên cứu của L.L.Thurstone được thực hiện bằng một con đường “quan sát mẫu”. Bởi vậy, nghiên cứu sẽ gây ra hạn chế khi thực nghiệm trên người bị khiếm thị. Trên thực tế, những người khiếm thị vẫn có thể phát triển tư duy không gian mà không cần trực tiếp hình dung thế giới thực bằng hình ảnh [5].

Howard Gardner chỉ ra cốt lõi của trí thông minh không gian (spatial intelligence) chính là khả năng nhận biết thị giác một cách chính xác, thực hiện chuyển đổi và sửa đổi nhận thức và để có thể tái tạo các khía cạnh của trải nghiệm thị giác của một người, ngay cả khi không có sự kích thích vật lí liên quan [5]. Ông đưa ra các thành phần của trí không thông minh không gian bao gồm:

i) Năng lực tri giác không gian,

ii) Năng lực tưởng tượng ra sự dời chỗ hoặc thay thế của các bộ phận trong một hình,

iii) Năng lực xoay hình thầm trong óc,

iv) Năng lực định hướng không gian và năng lực xem xét các mối quan hệ không gian.

Trong đó năng lực tri giác kể đến các tính chất như bất biến của tri giác: nhận ra một số đặc điểm của vật thể là độc lập về chất liệu, màu sắc và vị trí trong không gian… Bản thân ông cũng khẳng định trí thông minh không gian (spatial intelligence) và các nghiên cứu khác về tư duy không gian (spatial thinking) tiêu biểu là nghiên cứu của L.L.Thurstone đều có những điểm giống nhau khác định chỉ có sự sai khác về tên gọi và phạm vi nghiên cứu mà tác giả hướng đến.

Theo Van Hieles [8], tư duy hình học (geometric thinking) được chia thành 5 mức độ (5 levels):

Trình độ 1 (visual level): Ở trình độ này, trẻ nhận thức không gian là những gì tồn tại xung quanh chúng, các hình hình học được xem như là cái toàn bộ hơn là các thành phần, đặc điểm cấu thành chúng (số cạnh hay chiều dài của cạnh, số đo của góc). Trẻ đánh giá về các hình dựa trên tri giác các đối tượng, không bằng suy luận logic.

Trình độ 2 (analysis level): Xuất hiện khả năng phân tích hình dạng ở trẻ. Thông qua kinh nghiệm trong hoạt động thực tiễn và giáo dục, trẻ bắt đầu nhận thức các tính chất của hình hình học, các tính chất này là cơ sở để phân tách lớp các hình hình học.

Trình độ 3 (infomal level): Trẻ có thể đưa ra các phán đoán đúng về mối quan hệ giữa các hình hình học, phát biểu các điều kiện cần và đủ để một hình là hình vuông, hình chữ nhật, v.v…. Tuy nhiên, các phát biểu trên chưa ở được thể hiện ở dạng cặp logic giả thiết – kết luận.

Trình độ 4 (logic level): Trẻ có thể xác định chính xác giá trị chân lý của một mệnh đề về mối quan hệ giữa các hình hay giữa các tính chất của 1 hình hình học và các mệnh đề đảo, phản, phản đảo của nó.

Trình độ 5 (abstract level): Trẻ có khả năng nhận thức hệ tiên đề hình học đóng vai trò quyết định trong việc hình thành hình thức trừu tượng của phương pháp tiên đề, với sự trừu tượng hóa hoàn toàn đối với bản chất của các đối tượng và các quan hệ được nói tới trong lý thuyết tiên đề hóa.

Ở trình độ 1, trẻ có xu hướng phát huy trí thông minh không gian (spatial intelligence) hơn là tư duy logic, thời điểm mà trẻ chưa được học về cấu trúc chặt chẽ của các khái niệm cũng như phương pháp tiên đề trong hình học. Trẻ có khả năng thực hiện các thao tác xoay hình, dời hình, tìm mặt khuất của hình, … nhằm biến đổi các biểu tượng không gian. Ở các trình độ cao hơn, trẻ phát triển tư duy logic hơn khi phát hiện các đặc tính của các hình hình học.

Theo Pinkernell [13], mô hình của tiềm năng không gian (spatial ability) được cấu tạo bởi thành tố không gian – thị giác (spatial – visual operations), tư duy hình học (geometric thinking), tiềm năng hình ảnh (visual abilities). Trong đó, thành tố không gian – thị giác bao gồm khả năng xây dựng hoặc tái tạo các đối tượng, để biến đổi các đặc điểm không gian – hình ảnh của chúng. Tư duy hình học bao gồm khả năng nhận biết và hiểu các đối tượng không gian, mô tả chúng và hình biến đổi của chúng được xem xét dựa trên đặc điểm hình học. Cuối cùng, tiềm năng hình ảnh là sự diễn giải và xây dựng các dạng biểu diễn khác nhau của các đối tượng không gian.

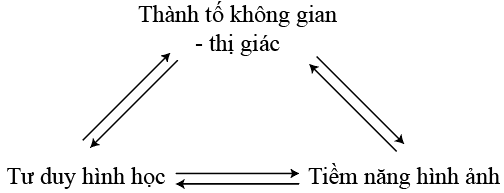
Mô hình tiềm năng không gian, Pinkernell

Angle Mizze nhận xét tư duy hình học (geometric thinking) trong mô hình mà Pinkernell đã nêu đóng vai trò quan trọng trong việc thể hiện và phát triển tiềm năng không gian trong các lớp học toán [11].

Theo chúng tôi những năng lực thành phần dưới đây cần được quan tâm để phát triển tư duy hình học ở trẻ em:

F1. Năng lực quan sát và tái tạo hình ảnh của đối tượng dựa vào các đặc điểm hình học;

F2. Năng lực định hướng không gian và tưởng tượng sự thay thế hoặc rời chỗ bộ phận của đối tượng.

Những hoạt động nào góp phần phát triển tư duy hình học?

Theo P.Ia.Galperin, hành động với đồ vật hay với vật chất hóa, tức là hành động với các biến thể  của nó như hình vẽ, sơ đồ, mô hình, hình mẫu… của vật thật đó là nguồn gốc của mọi hành động trí tuệ trọn vẹn. Mục đích của nó là phân tích, tách nội dung đích thực của hành động tâm lý nằm trong đối tượng vật thật (hay vật chất hóa). Nội dung của bước này là chủ thể dùng tay để triển khai hành động, luyện tập, khái quát và rút gọn nó. Như vậy chính hành động với đồ vật, hành động bên ngoài là cơ sở để hình thành thao tác ở giai đoạn tiếp theo ở trẻ [12].

Theo Piaget và Inhelder [14], trẻ em “chỉ có thể trừu tượng ý tưởng về mối quan hệ bình đẳng trên cơ sở hành động về sự bình đẳng, ý tưởng về đường thẳng đến từ hoạt động đi theo bàn tay hoặc mắt mà không đổi hướng, và ý tưởng về một góc đến từ hai chuyển động giao nhau”. Cụ thể, nhận thức của trẻ về hình dạng không đến từ việc tìm kiếm thụ động mà đến từ cảm nhận của cơ thể như bàn tay, mắt … và tâm trí của trẻ, … tham gia vào hành động. Ngoài ra, thí nghiệm minh họa cho thấy trẻ em cần khám phá các hình hình học bằng trải nghiệm để hiểu đầy đủ các đặc tính của chúng [2].

Trong các nghiên cứu của Clements [1], Greabell [6] cũng cho thấy những lợi ích to lớn của việc sử dụng đa dạng hoạt động thao tác bằng tay để giúp trẻ học về không gian và các hình hình học từ đó phát triển tư duy hình học.

Theo những nghiên cứu của chúng tôi để phát triển tư duy hình học cần cho trẻ thao tác trên các vật thật, bối cảnh thật thông qua các hoạt động học tập hấp dẫn.

2.2 Trò chơi Trí uẩn

Trí Uẩn là bộ đồ chơi do Nguyễn Trí Uẩn (1916-1995) một trí thức nổi tiếng của Việt Nam sáng tạo vào những năm 40 của thế kỉ 20, người ta dùng tên ông đặt tên luôn cho nó: Bộ trò chơi Trí Uẩn. Bộ đồ chơi này gồm 7 mảnh được cắt ra từ một hình chữ nhật có kích thước 72mmx90mm theo những nhát cắt xác định để tạo ra: một hình ngũ giác, hai tam giác vuông cân giống nhau, và 4 hình thang vuông (trong đó có hai hình thang vuông nhỏ giống nhau, hai hình thang vuông khác lớn hơn và sai khác nhau đúng một hình vuông (quan sát hình vẽ).

Hình 2.2.1 – Mô hình bộ đồ chơi Trí Uẩn

Bộ đồ chơi này có thể được làm bằng giấy, bìa cứng, bằng gỗ. Những người chơi sau này đã sáng tạo ra muôn vàn hình dạng khác nhau từ 7 mảnh gỗ ấy, với các chủ đề con người, lao động, công trình, động vật, thực vật đến các chữ cái hay các chữ số. Theo những thống kê không đầy đủ, người ta đã tạo ra khoảng 1500 hình dạng như vậy, và con số này không dừng ở đó mà vẫn đang nhiều thêm từng ngày [17, 18, 19].

Trong nghiên cứu của chúng tôi, Bộ Trí Uẩn được khai thác và sử dụng trong tổ chức các hoạt động hình học. Chúng tôi đặt tên các miếng ghép của bộ trò chơi Trí Uẩn lần lượt là X, Y, Z, T, U, K và V, đồng thời đánh số các cạnh và các góc của mỗi miếng ghép như hình 2.2.2 dưới đây

Hình 2.2.2 – Hình đánh số cạnh và góc của mỗi miếng ghép trong bộ trò chơi Trí Uẩn

Quy ước:  là cạnh 1 của miếng ghép K;  là góc 1 của miếng ghép K, d là trục đối xứng của bộ trò chơi Trí Uẩn.

Bảng sau mô tả quan hệ bằng nhau, quan hệ vuông góc, quan hệ song song xuất hiện trên bộ trò chơi Trí Uẩn:

Bảng 2.2.1 – Bảng mô tả quan hệ bằng nhau, quan hệ vuông góc,

quan hệ song song và quan hệ đối xứng trong bộ trò chơi Trí Uẩn

Tài liệu tham khảo

[1] Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning. In D. A.Grouws (Ed.), Handbook of research on mathematics teachingan’ learning (pp. 420-464). NewYork: Macmillan.

[2] Clements, Douglas H. (1998). Geometric and spatial thinking in young children. National Science Foundation, Arlington, VA.

[3] Brent Davis et al. (2015). Spatial reasoning in the early years. Principles, Assertions and Speculations. Routledge.

[4] Ekstrom et al. (1979). Cognitive factors: Their identification and replication. Educational Testing Service.

[5] Gardner, H. (1993). Frames of mind: The Theory of Multiple Intelligences. BasicBooks.

[6] Greabell, L. C. (1978). The effect of stimuli inputon the acquisition of introductory geometric concepts by elementary schoolchildren. School Science and Mathematics,71(4), p.320-326.

[7] Guttman, R., Epstein, E.E., Amir, M., Guttman, L., (1990). A Structural Theory of Spatial Abilities, Applied Psychological Measurement, vol. 14, No. 3, pp. 217-236.

[8] Van Hiele, P. M. (1986). Structure and insight: A theory of mathematics education. Orlando: Academic.

[9] Nguyễn Bá Kim (2011), Phương pháp dạy học môn Toán. Nhà xuất bản Đại học Sư Phạm Hà Nội.

[10] Luật Giáo dục năm 2015, Nhà xuất bản Chính trị Quốc Gia.

[11] Mizzi, A. (2017). The Relationship between Language and Spatial Ability. Essener Beiträge zur Mathematikdidaktik.

[12] Phan Trọng Ngọ (chủ biên), Nguyễn Đức Hướng (2003). Các lý thuyết phát triển tâm lý người, Nhà xuất bản Đại học Sư phạm Hà Nội, Hà Nội.

[13] Pinkernell, G. (2003). Räumliches Vorstellungsvermögen im Geometrieunterricht: Eine didaktische Analyse mit Fallstudien. Hildesheim: Franzbecker.

[14] Piaget, J., & Inhelder, B. (1967). The child’s conception of space. New York: W. W. Norton.

[15] Thurstone, L. L. (1950). Some primary abilities in visual thinking. Proceedings of the American Philosophical Society, 94(6), 517−521.

[16] Nguyễn Mạnh Tuấn (2013). Phát triển tư duy hình học cho trẻ mẫu giáo lớn và học sinh tiểu học qua một số hoạt động hình học. Luận án Tiến sĩ giáo dục học. Trường Đại học Sư phạm Hà Nội.

[17] Nguyễn Trí Uẩn (1957). Trí Uẩn: Trò chơi 7 quân chắp ra 1000 hình: Sách đố. Thư viện Quốc Gia Việt Nam.

[18] Nguyễn Trí Uẩn (1959). Trò chơi Trí Uẩn. Thư viện Quốc Gia Việt Nam.

[19] Nguyễn Trí Uẩn (1960). Tân Trí Uẩn. Thư viện Quốc Gia Việt Nam.

Xem tiếp: https://pomath.vn/tiem-nang-phat-trien-tu-duy-hinh-hoc-cho-tre-em-thong-qua-tro-choi-tri-uan-p3.html