Như đã hứa ở số trước, trong bài viết này POMath sẽ giới thiệu đến các độc giả cách sáng tạo ra khối tứ diện đều và khối bát diện đều.

Chuẩn bị: 6 mảnh giấy hình chữ nhật đồng (bronze rectangle) là hình chữ nhật được tạo ra như sau:


Bây giờ chúng ta sẽ tìm hiểu cách gập những mảnh giấy này thành các mảnh cơ sở hình tam giác. Từ tờ giấy hình chữ nhật đồng có thể gập được hai loại mảnh cơ sở tam giác: Loại A và Loại B.

Ghi chú:
01: Sử dụng một mảnh hình chữ nhật đồng
02: Gập góc dưới bên trái của hình chữ nhật đồng lên góc phải bên trên.
03: Mở đường vừa gập ra ta có thể nhìn thấy đường nếp gập EF
04: Gập góc trái bên dưới A lên trùng với điểm E, sao cho cạnh FA trùng với đường nếp gập EF.
05: Gập góc trên bên phải C xuống trùng với điểm F, sao cho cạnh EC trùng với nếp gập EF.
Hình gập xong là một hình bình hành với khe ở đường chéo.
08:Lật ngược mảnh giấy (không nhìn thấy khe đường chéo) gập đoạn thẳng D’F lên trên đoạn thẳng A’F.
09: Gập tiếp đoạn thẳng EA’ lên trên đoạn thẳng đứng bên phải. Ta nhận được một hình thoi.
10: Lật ngược hình thoi lại
11: Gấp đôi hình thoi ở đường chéo ngắn sao cho đường khe ở mặt ngoài.
12: Mở các đường vừa gấp ra, ta đã chia hình
Mảnh cơ sở tam giác loại B.

Để chuẩn bị ghép hình tứ diện đều và hình bát diện đều, các bạn hãy gấp 5 mảnh cơ sở tam giác loại A và 1 mảnh cơ sở tam giác loại B từ 6 miếng bìa hình chữ nhật đồng đã chuẩn bị trước đó nhé! Bây giờ chúng ta sẽ sử dụng một mảnh cơ sở tam giác loại A và một mảnh cơ sở tam giác loại B và thực hiện theo các bước sau để ghép hình tứ diện đều nào!
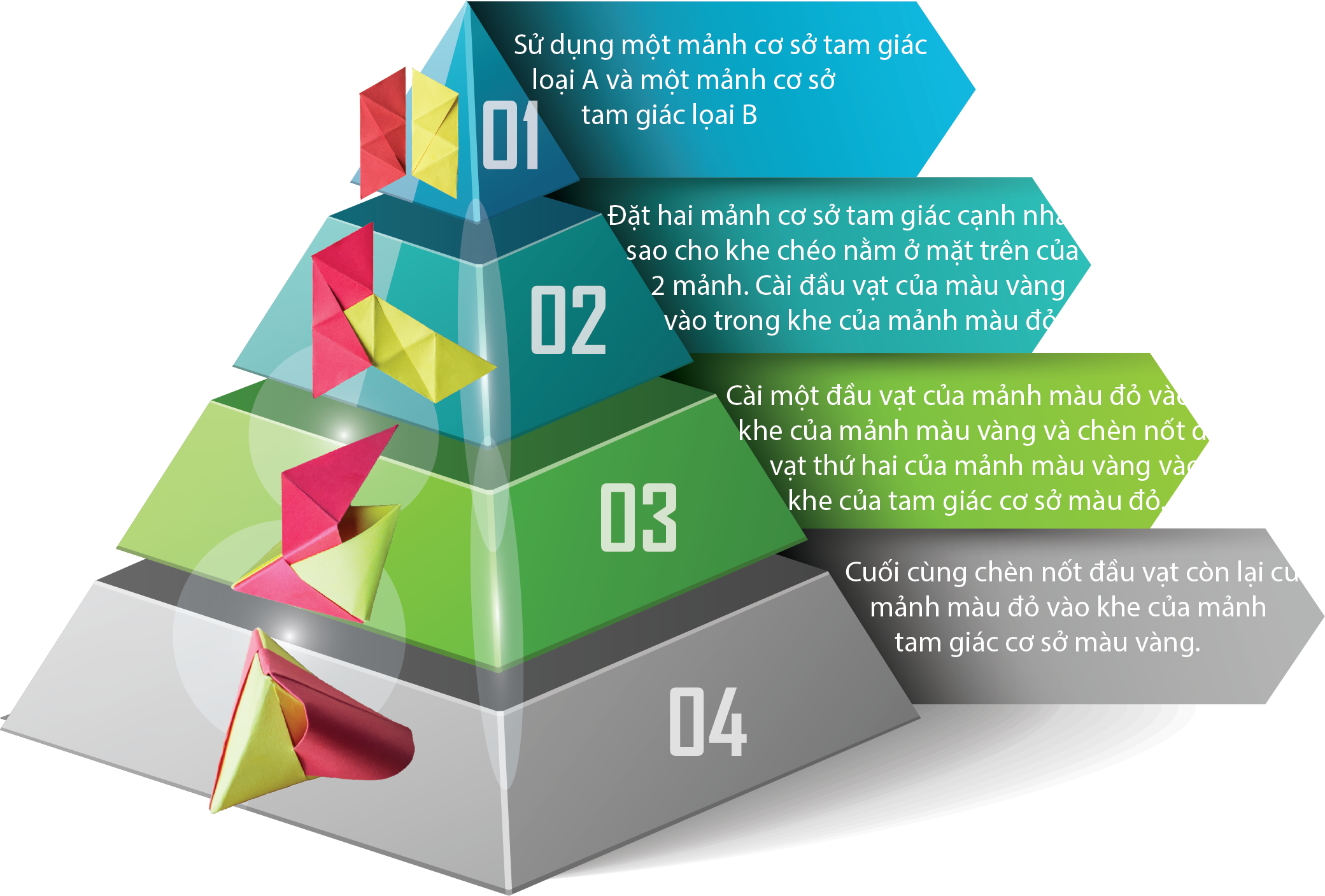
Vậy là các bé đã gấp được một khối hình tứ diện đều. Các bé biết không, tứ diện đều là khối đa diện có 4 đỉnh, 6 cạnh và 4 mặt là 4 tam giác đều bằng nhau và khối tứ diện đều trong Toán học được kí hiệu là {3;3}. Trong xây dựng, ta có thể bắt gặp rất nhiều các khối hình, công trình được xây dựng dựa theo hình tứ diện đều. Trong tự nhiên cũng vậy, khi nghiên cứu cấu trúc của nước để trả lời câu hỏi: “Tại sao nước ở nhiệt độ dưới 0 độ C lại rắn đến vậy?”. Ta cũng bắt gặp được khối hình tứ diện với bốn đỉnh là các phân tử nước (H-O-H). Bởi sự cân xứng, hài hòa nên khi các phân tử nước đá kết hợp với nhau tạo thành một mạng tinh thể hình tứ diện đều lại có một cấu trúc vô cùng vững chắc.
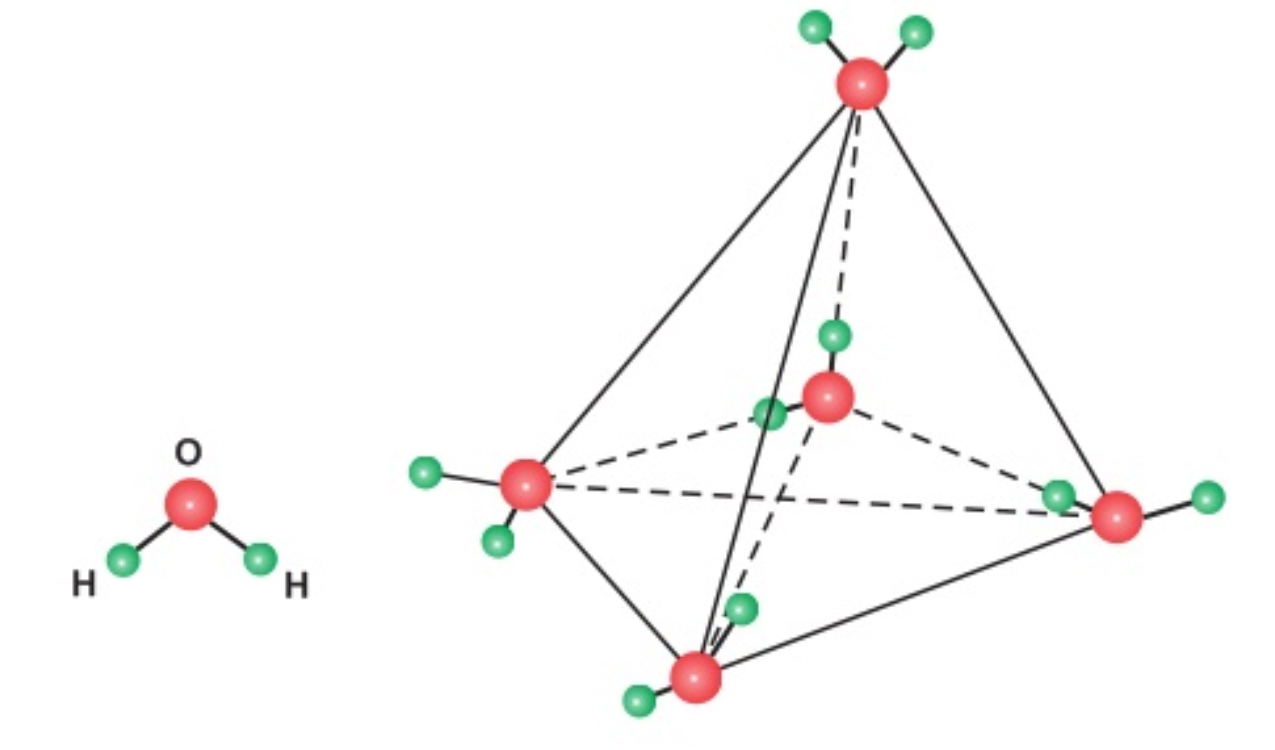

Mô hình mạng tinh thể phân tử nước đá
Bây giờ chúng ta sẽ sử dụng 4 mảnh cơ sở tam giác loại A còn lại để ghép khối bát diện đều:

Khối bát diện đều: là một đa diện lồi đều với 6 đỉnh, 12 canh, 8 mặt, mỗi mặt là một tam giác đều. Khối bát diện đều trong toán học được kí hiệu là {3, 4}. Các em biết không, những viên kim cương siêu cứng và đẹp long lanh chính vì nó có cấu trúc tinh thể bát diện đều đấy!
Như vậy các em đã học được cách gấp khối tứ diện đều và khối bát diện đều từ các hình chữ nhật đồng. Hy vọng các em đã có khoảng thời gian trải nghiệm toán học và nghệ thuật thật vui vẻ.
Toán tư duy POMath – Trung tâm toán trải nghiệm dành cho trẻ:
? Hotline: 0974.838.877
? Website: https://POMath.vn/
? Fanpage: https://www.facebook.com/pomathvietnam/


